Лекция 7. Битовые поля и побитовые операции¶
Системы счисления¶
Теория¶
Системы счисления¶
В настоящее время применяются позиционные системы счисления, изобретённые в Древней Индии.
Основные используемые системы счисления:
- Двоичная (алфавит \(A_2={0,1}\) ).
- Десятичная (алфавит \(A_{10}={0,1,2,3,4,5,6,7,8,9}\) ).
- Шестнадцатеричная (алфавит \(A_{16}={0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f}\) ).
Принцип формирования числа:
\(n = a_{m-1}(o)^{m-1}+...+a_1(o)+a_0\)
\(o\) - основание системы счисления (2,10,16).
\(a\) - значение разряда.
\(m\) - номер разряда.
Пример:
\(234 = 2*10^2+3*10^1+4*10^0\)
Перевод из двоичной в десятичную¶
Пример
Имеем двоичное число \(n_{2}=00101001\) .
\(o=2, m=8\)
Ему соответствует десятичное \(n_{10}=0*(2)^7+0*(2)^6+1*(2)^5+0*(2)^4+1*(2)^3+0*(2)^2+0*(2)^1+1*(2)^0=32+8+1=41\)
Числа, содержащие по одной единице легко запоминаются:
| \(00000001\) | \(1\) |
| \(00000010\) | \(2\) |
| \(00000100\) | \(4\) |
| \(00001000\) | \(8\) |
| \(00010000\) | \(16\) |
| \(00100000\) | \(32\) |
| \(01000000\) | \(64\) |
| \(10000000\) | \(128\) |
Несложно выполнить перевод, если числа содержат несколько идущих подряд единиц:
| \(00000011\) | \(4-1=3\) |
| \(00000111\) | \(8-1=7\) |
| \(00001111\) | \(16-1=15\) |
| \(00011111\) | \(32-1=31\) |
| \(00111111\) | \(64-1=63\) |
| \(01111111\) | \(128-1=127\) |
| \(11111111\) | \(256-1=255\) |
Перевод из десятичной в двоичную¶
Пусть дано \(n_{10}=57\)
- Разделить 57 на 2: 28 - 1 (с остатком)
- Разделить 28 на 2: 14 - 0 (без остатка)
- Разделить 14 на 2: 7 - 0 (без остатка)
- Разделить 7 на 2: 3 - 1 (с остатком)
- Разделить 3 на 2: 1 - 1 (с остатком)
- Разделить 1 на 2: 0 - 1 (с остатком)
Пишем значения разрядов в обратном порядке.
В результате получаем \(n_2=111001\) .
Перевод из шестнадцатиричной в десятичную¶
Пример
\(2a = 2*16^1+a = 32+10 = 42\)
Пример
\(ff = f*16^1 +f = 15*16+15 = 255\)
Перевод из шестнадцатиричной в двоичную¶
Удобно переводить шестнадцатиричное число в двоичное по тетрадам:
Пример
Рассмотрим число \(8a\)
| \(8\) | \(a\) |
| \(1000\) | \(1010\) |
Ответ: \(10001010\)
Порядок байтов¶
Little Endian vs. Big Endian¶

Используется два порядка расположения байтов в многобайтной величине: от старшего к младшему big endian и от младшего к старшему little endian.
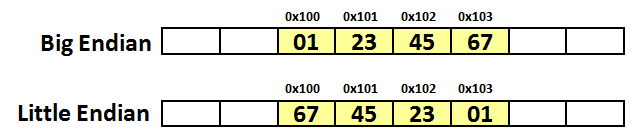
BE используют: IBM 360/370/390, Motorola 68000, SPARC
LE используют: Intel x86
Достоинства LE¶
Существенным достоинством little-endian по сравнению с big-endian порядком записи считается возможность ‘’неявной типизации’’ целых чисел при чтении меньшего объёма байт.
Так, если в ячейке памяти содержится число 0x00000022, то прочитав его как int16 (два байта) мы получим число 0x0022, прочитав один байт — число 0x22. Однако, это же может считаться и недостатком, потому что провоцирует ошибки потери данных.
Проверка¶
Следующие функции позволяют проверить, какой порядок байт принят в вашей системе:
int endian1() {
int one = 1;
char *ptr;
ptr = (char *)&one;
return (*ptr);
}
int endian2() {
union {
int one;
char ch;
} endn;
endn.one = 1;
return endn.ch;
}
Использование полей битов¶
Очень полезное с практической точки зрения представление памяти в 1 байт, которое можно использовать как unsigned char или как набор значений отдельных битов.
union CODE
{
unsigned char ch;
struct BYTE
{
unsigned b1:1;
unsigned b2:1;
unsigned b3:1;
unsigned b4:1;
unsigned b5:1;
unsigned b6:1;
unsigned b7:1;
unsigned b8:1;
} byte;
};
Функция, переводящая байт из 10-тичной системы в 2-ичную с использованием поля битов:
void bin(unsigned char c)
{
union CODE code;
code.ch=c;
printf("Bit numbers: 8 7 6 5 4 3 2 1 \n");
printf("Bit values: %d %d %d %d %d %d %d %d ",
code.byte.b8,
code.byte.b7,
code.byte.b6,
code.byte.b5,
code.byte.b4,
code.byte.b3,
code.byte.b2,
code.byte.b1);
printf("Number: %d Symbol: %c\n",c,c);
}
Побитовые операции¶
Обзор¶
Побитовые операции¶
Побитовые операции применяются к значениям отдельных разрядов числа и их не следует путать с обычными логическими операциями (&&, ||,!), которые действуют на значение в целом.
- & - умножение (конъюнкция)
- \(|\) - сложение (дизъюнкция)
- ~ - отрицание
- \(>>\) - побитовый сдвиг вправо
- \(<<\) - побитовый сдвиг влево
- \(^ \) - исключающее “или” (xor)
Вместе с этими операциями может использоваться присваивание, например a>>=2
Отрицание¶
Поразрядное отрицание alert{~{ меняет значение битов на противоположное
unsigned char a=4; (00000100)
unsigned char b=~a; (11111011)
Следующая функция возвращает максимальное значение unsigned int в вашей системе:
typedef unsigned int ui;
ui getMaxUIValue()
{
return ~(ui)0;
}
Поразрядное ‘’И’‘¶
Операция & ‘’И’’ является бинарной и выставляет результирующий бит в 1, если оба бита операндов равны 1.
Поразрядное И¶
Преобразование числа в бинарную форму:
void binary(ui n)
{
for(int i = 256; i > 0; i /=2) {
if(n & i)
putchar('1');
else
putchar('0');
}
putchar('\n');
}
Поразрядное ‘’ИЛИ’‘¶
Операция | ‘’ИЛИ’’ является бинарной и выставляет результирующий бит в 1, если хотя бы один бит у операндов равен 1.
Поразрядное ИСКЛЮЧАЮЩЕЕ ИЛИ¶
Операция ** \(\widehat{**\) } ‘’ИСКЛЮЧАЮЩЕЕ ИЛИ’’ является бинарной и выставляет результирующий бит в 1, если первый (или второй) бит операнда равен 1, но не оба одновременно.
XOR¶
В следующем примере XOR используется для обмена значений двух целочисленных переменных:
void swap(int *a,int *b)
{
*a=*a^*b;
*b=*a^*b;
*a=*a^*b;
}
Полезные мелочи¶
Проверка, выставлен ли данный бит:
int getBit(int n, int index)
{
return ( (n & (1 << index) ) > 0);
}
Подсчёт количества выставленных битов:
int bitCountA(int n)
{
int count = 0;
while(n) {
if(n & 1) count++;
n = n >> 1;
}
return count;
}
Очистка заданного бита:
unsigned char b &= ~(1 << n);
Переключение бита:
unsigned char c ^= (1 << n);
Выделение первого и второго байтов:
unsigned char right = val & 0xff;
unsigned char left = (val>>8) & 0xff;
Выделение знакового разряда:
char sign = val & 0x8000;
Маски¶
Маска - это битовый шаблон с установленными значениями разрядов.
Если найти результат операции ‘’И’’ между величиной и маской, то в результате получим только те значения разрядов, у которых маска содержала единицы:
В данном примере из 24-битной величины выделяется первый байт.
При необходимости можно включить специфические биты, не изменяя оставшиеся. Это произойдет, если наложить маску с помощью операции |.
flags |= MASK;
Аналогично можно отключить избранные разряды:
flags &= ~MASK;
Приведем пример с переключением значения битов (установкой в ноль единиц):
flags ^= MASK;
Для сравнения значения разряда необходимо сначала маскировать другие биты
if((flags & MASK)==MASK) {
...
}
Вопросы для самоконтроля¶
- Опишите принцип формирования числа в позиционной системе счисления.
- Перечислите наиболее распространенные системы счисления.
- Как перевести число из двоичной системы в десятичную?
- Как перевести число из десятичной системы в двоичную?
- Как перевести шестнадцатиричное число в десятичное?
- Как перевести шестнадцатиричное число в двоичное?
- Как узнать, какой порядок байт в вашей системе?
- Как можно перевести число в двоичную систему без деления?
- Перечислите побитовые операции.
- Чему равен результат поразрядного отрицания?
- Как узнать максимальное значение целого беззнакового типа в системе?
- Чему равен результат поразрядного И?
- Чему равен результат поразрядного ИЛИ?
- Чему равен результат поразрядного исключающего ИЛИ?
- Как реализовать обмен двух целых без вспомогательной ячейки?
- Что такое маска? Для чего могут использоваться маски?
- Как включить и выключить специфические разряды?
- Как можно переключить значение бита? Сравнить значение бита?