Лекция 8. Динамическая организация данных¶
Динамическая память¶
Введение¶
Динамическое распределение памяти¶
- Происходит во время выполнения программы (run-time)
- Объем ограничивается размером виртуальной памяти ЭВМ
- Размер может переопределяться
- Выделение и освобождение может происходить в любом месте программы
- Объявить указатель на желаемый тип
- Запросить блок желаемого размера
- Проверить результат запроса
- Использовать
- Освободить
Функции¶
Функции для работы с ДП¶
| Прототип | Назначение |
| void * malloc (size_t size) | выделяет блок размером size байт |
| void * calloc(size_t n, size_t size) | выделяет обнуленный блок для хранения n-элементов по size байт |
| void * realloc(void* ptr, size_t size) | переопределяет размер блока |
| void free(void *ptr) | освобождает блок памяти |
Пример использования malloc¶
int *arr1=(int *)malloc(N*sizeof(int));
char *arr2=(char*)malloc(M*sizeof(char));
if(!arr1 || !arr2)
{
puts("Memory allocation error!");
exit(1);
}
..
free(arr1);
free(arr2);
Пример использования сalloc¶
int *arr1=(int *)calloc(N,sizeof(int));
char *arr2=(char*)calloc(M,sizeof(char));
if(!arr1 || !arr2)
{
puts("Memory allocation error!");
exit(1);
}
..
free(arr1);
free(arr2);
Пример с чтением файла¶
Сначала определяется размер файла, а потом он считывается целиком в подготовленный буфер.
FILE *fp=fopen(argv[1],"rt");
if(!fp) { puts("File error!"); exit(1); }
long len=0;
fseek(fp,0L,SEEK_END);
len=ftell(fp);
char *buf=(char*)malloc(len*sizeof(char));
if(!buf) { puts("Memory error!"); exit(2); }
fseek(fp,0L,SEEK_SET);
fread(buf,sizeof(char),len,fp);
..
fclose(fp);
free(buf);
Массивы¶
Многомерные массивы¶
Создание двумерного динамического массива происходит в два этапа: сначала создается массив указателей, затем с каждым из указателей связывается одномерный массив.
float **arr=(float**)malloc(N*sizeof(float*));
for(i=0;i<N;i++)
arr[i]=(float*)malloc(M*sizeof(float));
Уничтожение массива происходит в обратном порядке:
for(i=0;i<N;i++)
free(arr[i]);
free(arr);
Ошибки¶
Ошибки, связанные с памятью¶
По различным данным, до 90% всех сбоев в программах на С/С++ возникает в связи с неправильным обращением к памяти. При работе с ДП возможны следующие виды ошибок:
- Утечки памяти (memory leaks)
- Ошибочные запросы на выделение
- Повторное освобождение
- Выход за границы выделенной памяти
Пример с двойным освобождением¶
void fun(int *p)
{
...
free(p);
}
int main()
{
int *arr=(int*)malloc(N*sizeof(int));
...
fun(arr);
free(arr); // Ошибка!
...
}
Пример с утечкой памяти¶
void alloc(int * arr, int N)
{
arr=(int*)calloc(N,sizeof(int));
}
int main()
{
int *arr=NULL;
alloc(arr);
...
free(arr); // error!
...
}
float **arr=(float**)malloc(N*sizeof(float*));
for(i=0;i<N;i++)
arr[i]=(float*)malloc(M*sizeof(float));
...
free(arr);
Пример пожирателя памяти¶
Данная программа безостановочно ‘’пожирает’’ динамическую память, вызывая проблемы в ОС.
int main()
{
while(1)
{
double *ptr;
ptr=(double*)malloc(10000*sizeof(double));
}
return 0;
}
Динамические структуры¶
Фундаментальные структуры данных¶
Существуют два фундаментальных способа организации данных:
- Массив - набор элементов одного типа, следующих в памяти друг за другом.
- Запись - набор элементов разного типа, следующих в памяти друг за другом.
Замечательно то, что массивы и записи можно объединять, создавая:
- Массивы записей.
- Записи, содержащие массивы.
На основе массивов и записей строят:
- Связанный список - набор элементов одного типа, не обязательно следующих в памяти друг за другом и связанных между собой благодаря хранению адресов.
- Графы - множество вершин (узлов), соединённых рёбрами.
- Деревья - иерархически связанные элементы данных, частный случай графа.
- Хэш-таблицы (ассоциативные массивы) - наборы ‘’ключ-значение’‘.
- Очереди - ‘’First in First out’‘.
- Стеки - ‘’Last in, First out’‘.
- Деки - двусвязные очереди.
- Очереди с приоритетами.
Недостатки массивов¶
Достоинства и недостатки массивов¶
Достоинства массива:
- простота организации,
- высокая скорость доступа к элементам ( \(O(1)\) ).
Недостатки:
- сложность операций добавления и удаления элементов,
- требуется непрерывный участок памяти,
- опасности, связанные с выходом за границы.
Недостатки массивов¶
Для вставки элемента в массив необходимо произвести поэлементное копирование с целью освобождения позиции для вставки. Чем далее позиция от конца массива, тем больше операций копирования
Проблема статического массива
Размер массива ограничен и не может быть переопределён в процессе работы программы. В результате данные не могут быть добавлены в уже заполненный массив
Проблема динамического массива
Добавление новых элементов требует выделения нового участка памяти, копирования элементов из старого массива, освобождения старого участка памяти. В результате страдает производительность программы
Связанные списки¶
Понятие списка¶
Понятие связанного списка¶
Определение
Связанный список - это способ организации данных, при котором элементы данных хранят адреса соседних элементов.
Связанный список является альтернативой массиву для хранения набора однотипных данных.
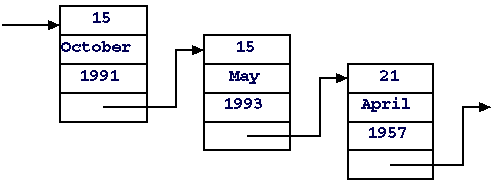
Классификация списков¶
Существует несколько разновидностей связанных списков:
- Односвязные - связь только от предшествующего к последующему.
- Двусвязные - связь в обоих направлениях.
- Кольцевые - от последнего элемента мы вновь переходим к первому.
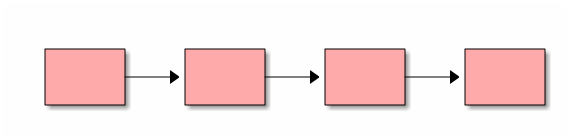
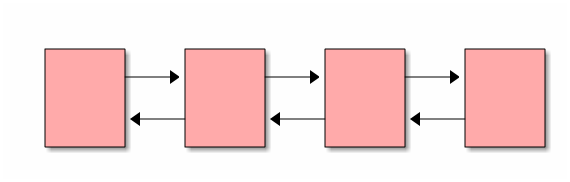
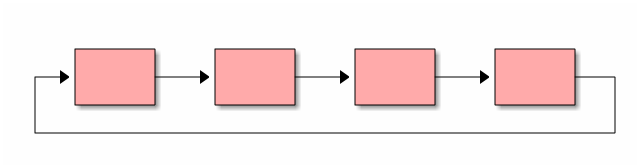
Терминология списков¶
- List - список.
- Item - элемент списка.
- Head - головной (первый) элемент списка.
- Tail - хвостовой (последний) элемент списка.
- Link - cвязь.
- Next - указатель на следующий элемент.
- Prev - указатель на предыдущий элемент.
- NULL - маркер нулевого адреса.
Достоинства и недостатки списков¶
Связные списки устраняют недостатки массива, при этом сложность алгоритма нахождения заданного элемента равна \(O(n)\) . Платой за эффективность использования памяти является наличие дополнительных процедур по построению и поддержанию целостности списка. Особенностью списка по сравнению с массивами является хранение адресов связанных элементов в каждом элементе.
Пример:
На платформе Win32, односвязный список, состоящий из 1000 элементов будет дополнительно расходовать 4000 Байт памяти, независимо от размера хранимых данных.
Анатомия списка¶
Методы программной реализации списков¶
Для описания элемента списка (item) в С и C++ используется понятие структуры, которая описывается ключевым словом tetxbf{struct}.
Можно описать два способа программной реализации списков:
- служебная информация помещается в одну структуру вместе с полезными данными;
- служебная информация выносится в отдельную структуру.
Рассмотрим пример организации элемента списка для хранения информации о событии
typedef unsigned char UC;
typedef unsigned short US;
struct EVENT
{
UC day; // день месяца
char mon[10]; // месяц
US year; // год
char buf[256]; // описание события
struct EVENT *next; // следующее событие
};
Обращаем внимание на то, что служебное поле next содержится в одной структуре с информационными полями.
Список, построенный из элементов типа EVENT будет выглядеть следующим образом:
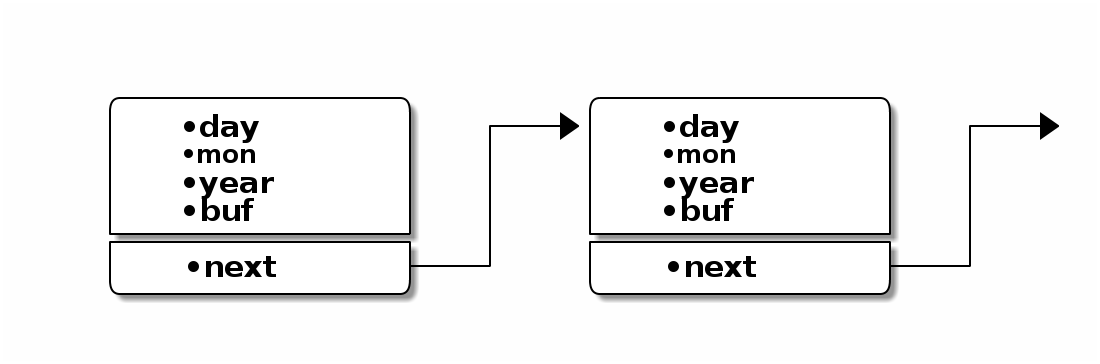
Второй метод реализации немного сложнее, зато отличается большей гибкостью
struct EVENT
{
UC day; // день месяца
char mon[10]; // месяц
US year; // год
char buf[256]; // описание события
};
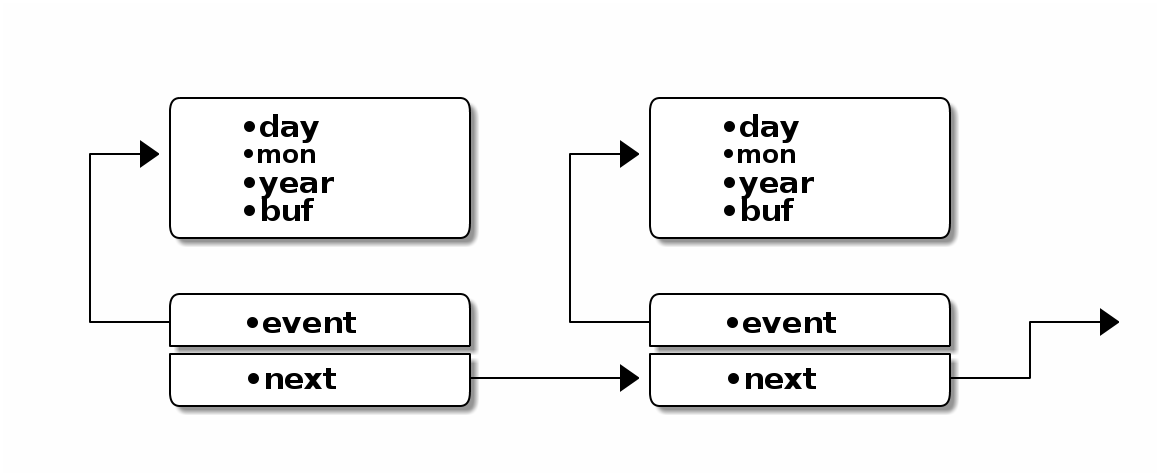
struct ITEM
{
struct EVENT *event; // адрес записи
struct ITEM *next; // следующий элемент
};
Схема списка при раздельной реализации
Набор операций¶
Для работы со списком необходимо определить набор операций (API - Application Programming Interface)
- create() - создание списка,
- access() - получение доступа к i-ому элементу в списке,
- add() - добавление нового элемента в список,
- remove() - удаление элемента из списка,
- count() - подсчет числа элементов в списке,
- save() - сохранение списка в файле,
- load() - чтение списка из файла,
- search() - поиск элемента по значению поля,
- union() - объединение двух списков в один,
- swap() - перестановка двух элементов списка,
- sort() - сортировка элементов по некоторому полю,
- copy() - создание копии списка
Функция create¶
Функция create создает новый список с одним элементом.
struct ITEM *create(struct EVENT *event)
{
struct ITEM *head=(struct ITEM*)malloc(sizeof(struct ITEM));
head->event=event;
head->next=NULL;
return head;
}
Функция add - добавление элемента¶
Добавление элемента в существующий список
void add(struct ITEM *head, struct EVENT *event)
{
while(head->next)
head=head->next;
head->next=(struct ITEM*)malloc(sizeof(struct ITEM));
head->next->event=event;
head->next->next=NULL;
}
Функция определяет хвостовой элемент (по значению NULL в поле next, затем создаёт новый элемент и включает его в список, делая хвостовым.
Функция remove - удаление элемента¶
Удаление элемента из списка, находящегося на позиции i
struct ITEM* remove(struct ITEM *head,int i)
{
struct ITEM *newhead=head,*temp;
// удаляем первый элемент, head меняется
if(i==0) {
newhead=head->next; // второй делается первым
}
else {
while(head->next) {
if(--i==0)
break; // обнаружили удаляемый элемент
head=head->next;
}
if(i>0)
return newhead; // удаляемого элемента не существует
else if(head->next) { // удаляем элемент из середины
temp=head->next; // удаляемый элемент
head->next=head->next->next;
free(temp); // освобождаем память
}
}
return newhead;
}
Функция print - печать элемента¶
Для того, чтобы распечатать заданный элемент, нам необходимо найти его в списке
void printItem(struct ITEM *head,struct ITEM *item)
{
while(head)
{
if(head==item) {
printEvent(head->event);
return;
}
head=head->next;
}
}
Основные сведения о деревьях¶
Понятие дерева¶
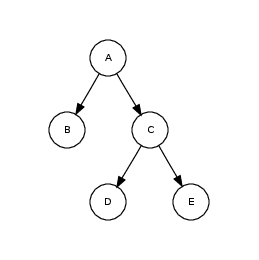
Дерево (англ. Tree) - иерархическая структура данных, состоящая из узлов, расположенных на уровнях и соединённых ветвями
Основное преимущество дерева перед списком: скорость доступа к информации.
Если в списке доступ осуществляется в среднем за \(O(N)\) , то в бинарном дереве: \(O(log_2(N))\)
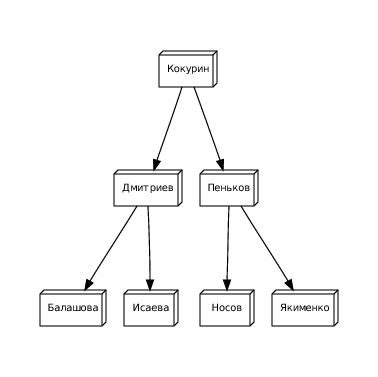
Задача: Проверить наличие среди сотрудников человека по фамилии Задорожный.
Для того чтобы установить отсутствие человека с этой фамилией в БД сотрудников необходимо проверить 3 элемента, а не 7, как в случае списка
Древовидная структура характеризуется множеством узлов, происходящих из единственного начального узла, называемого корнем. Сыновья узла и сыновья сыновей называются потомками узла, а родители и прародители - предками. Каждый некорневой узел имеет только одного родителя и каждый родитель имеет 0 и более сыновей. Узел, не имеющий детей, называется листом.
Каждый узел дерева является корнем поддерева, которое определяется данным узлом и всеми потомками этого узла.
Прохождение от родительского узла к его дочернему узлу и к другим потомкам осуществляется вдоль пути. Тот факт, что каждый некорневой узел имеет единственного родителя, гарантирует, что существует единственный путь из любого узла к его потомкам. Путь от корня к узлу дает меру, называемому уровнем узла. Уровень есть длина пути от корня к этому узлу.
Глубина дерева есть максимальный уровень любого его узла или длина самого длинного пути от корня до узла.

Для дерева, изображённого на рисунке:
- A - корневой узел (нулевой уровень).
- B,C - потомки первого уровня.
- D,E - потомки второго уровня.
- B,D,E - листы.
- Глубина дерева - 2.
Классификация деревьев¶
Деревья можно классифицировать:
по максимальному количеству потомков у одного узла:
- бинарные (2 потомка);
- тернарные (3 потомка);
- M-арные (M-потомков);
по структуре:
- симметричные;
- сбалансированные;
- несбаллансированные;
- полные;
- вырожденные;
по характеру данных:
- с упорядоченными данными;
- с неупорядоченными данными;
по виду:
- бинарные с упорядоченными данными (поиска);
- B-деревья;
- Красно-чёрные (с балансировкой);
Бинарные деревья¶
Основы¶
Бинарные деревья¶
Одним из наиболее распространенным видом деревьев являются бинарные, которые допускают разнообразные алгоритмы прохождения и эффективный доступ к элементам.
У каждого узла бинарного дерева может быть 0,1 или 2 потомка. По отношению к левому узлу применяется термин левый потомок, по отношению к узлу справа - правый потомок. Бинарное дерево является рекурсивной структурой. Каждый узел является корнем своего собственного поддерева.
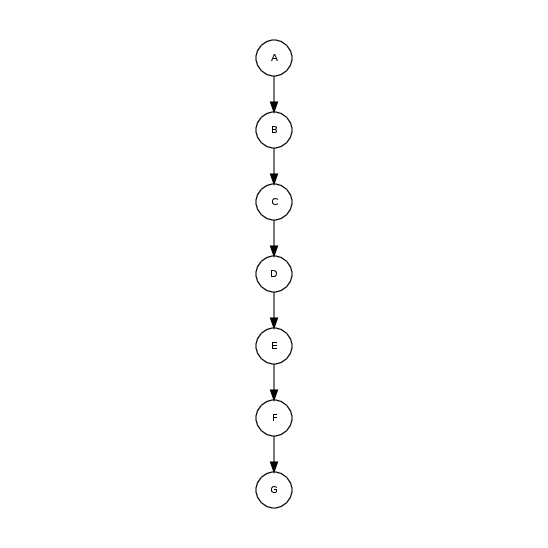
На любом уровне \(N\) бинарное дерево может содержать от \(1\) до \(2^N\) узлов. Вырожденным будет называться такое дерево, у которого один лист и каждый узел имеет одного сына. Вырожденное бинарное дерево эквивалентно связанному списку.
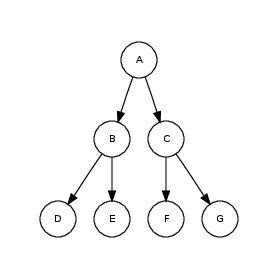
Вырожденные деревья являются крайней мерой плотности размещения данных в коллекции. Другая крайность - полные бинарные деревья, в них каждый узел имеет обоих потомков.
Полное дерево глубины 2:
Вырожденное дерево с теми же элементами:
Операции над деревом¶
Операции¶
Для бинарного дерева существует несколько операций, важнейшими из которых являются создание дерева, и обход его узлов. Обе процедуры рекурсивны.
Существует несколько методов прохождения дерева для доступа к его элементам. К ним относятся прямой, обратный и симметричный.
При прохождении дерева используется рекурсия, поскольку каждый узел является корнем своего поддерева. Каждый алгоритм выполняет в узле три действия: заходит в узел, рекурсивно спускается по левому и по правому поддереву. Спуск прекращается при достижении пустого поддерева (нулевой указатель).
Обход бинарного дерева¶
Порядок действий при прямом обходе:
- Обработка данных узла.
- Прохождение левого поддерева.
- Прохождение правого поддерева.
Порядок действий при обратном обходе:
- Прохождение левого поддерева.
- Прохождение правого поддерева.
- Обработка данных узла.
Порядок действий при симметричном обходе:
- Прохождение левого поддерева.
- Обработка данных узла.
- Прохождение правого поддерева.

Последовательность обработки узлов:
- прямой обход: ABDECFG
- симметричный обход: DBEAFCG
- обратный обход: DEBFGCA
Упорядоченные данные¶
При создании дерева часто используется свойство упорядоченности.
Свойство упорядоченности. Пусть \(x\) - произвольная вершина бинарного дерева. Если вершина \(y\) находится в левом поддереве вершины \(x\) , то
\(y \to data \le x \to data\) . Если вершина \(y\) находится в правом поддереве вершины \(x\) , то \(y \to data \geq x \to data\) .
В этом случае симметричный обход дерева позволяет обрабатывать элементы в порядке возрастания их значений. Именно этот принцип используется в двух рассматриваемых ниже программах обработки символов и строк.
Программная реализация¶
Структура бинарного дерева построена из узлов. Как и в связанном списке эти узлы содержат поля данных и указатели на другие узлы в коллекции. Узел дерева содержит поле данных и два поля с указателями, которые называются левым и правым указателями. Значение NULL является признаком пустого поддерева.
Пример описания узла бинарного дерева
struct TNODE
{
char symbol; // данные
long count; // счётчик
struct TNODE *left; // левый потомок
struct TNODE *right; // правый потомок
};
Основные операции¶
В качестве основных операций над элементами бинарного дерева можно предложить следующие:
- AddTree() - создание узла дерева и помещение в него данных,
- PrintTree() - печать дерева с данными в узлах,
- GoTree() - обход дерева (для обработки данных),
Создание дерева¶
Функция принимает два параметра - указатель на узел и код символа. Если указатель нулевой (находимся в листе дерева) выделяем память под узел и присваиваем указателям на потомков нулевые значения, а код символа и счетчик (равен 1) присваиваем информационным полям.
Если значение кода символа совпадает с данными в текущем узле увеличиваем значение счетчика на 1 и возвращаемся к родителю, если код меньше текущего, переходим к левому потомку (или к пустому указателю), а если код больше, то к правому.
В результате мы получим дерево, в котором каждому прочитанному из файла символу будет соответствовать свой узел, а поле count будет хранить число совпавших символов.
struct TNODE *AddTree(struct TNODE *node,char symbol)
{
if(node==NULL)
{
node=(struct TNODE*)malloc(sizeof(struct TNODE));
node->symbol=symbol;
node->count=1;
node->left=NULL;
node->right=NULL;
}
else if(symbol==node->symbol)
node->count++;
else if(symbol<node->symbol)
node->left=AddTree(node->left,symbol);
else
node->right=AddTree(node->right,symbol);
return node;
}
Пример: для строки tkrpaptzs дерево примет следующий вид
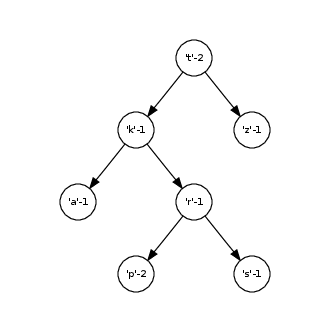
Обход дерева¶
Симметричный обход дерева
void GoTree(struct TNODE *node)
{
if(node) {
GoTree(node->left);
printf("%c\n",node->symbol);
GoTree(node->right);
}
}
Симметричный обход позволяет вывести символы в порядке возрастания значений.
Задача о 8 ферзях¶
Задача о расстановке ферзей
Расставить на шахматной доске 8 ферзей таким образом, чтобы они не находились под ударом друг друга. Найти все варианты решения этой задачи.
Идея решения этой задачи заключается в том, чтобы построить дерево, каждый узел которого отображал бы состояние одной клетки шахматной доски. Таким образом, у каждого узла может быть до 8 потомков (связи со следующей строкой доски).
Алгоритм:
- Нулевой уровень дерева содержит корень, у которого 8 потомков. Это означает, что на первую строку доски мы можем поставить ферзя в любую из 8 клеток.
- Далее все усложняется. Если мы ставим ферзя на первую клетку первой строки, выбор позиции на второй строке ограничен (например, нельзя ставить на 1,2 клетки). Тем не менее, у нас остается 6 вариантов.
- Выставив фигуру на второй строке доске, выбираем позицию на третьей.
- Процесс повторяется до тех пор, пока мы не дойдем до последней, восьмой строки. На ней существует только одна позиция для постановки ферзя.
- Рассматривая все варианты размещения фигуры на каждой строке, строим дерево.
Очевидно, что решением задачи является путь в дереве от корня до листа. Всего существует 92 пути.
Пример решения:
_______________________________
8 | | | | x | | | | |
|___|___|___|_ _|___|___|___|___|
7 | | x | | | | | | |
|___|___|___|___|___|___|___|___|
6 | | | | | | | x | |
|___|___|___|___|___|___|___|___|
5 | | | x | | | | | |
|___|___|___|___|___|___|___|___|
4 | | | | | | x | | |
|___|___|___|___|___|___|___|___|
3 | | | | | | | | x |
|___|___|___|___|___|___|___|___|
2 | | | | | x | | | |
|___|___|___|___|___|___|___|___|
1 | x | | | | | | | |
|___|___|___|___|___|___|___|___|
1 2 3 4 5 6 7 8
Вопросы для самоконтроля¶
- Перечислите свойства динамически выделенной памяти.
- Какой общий порядок работы с динамической памятью?
- Перечислите основные функции для работы с динамической памятью.
- Как прочитать файл целиком в динамический массив?
- Как создать динамический многомерный массив?
- Как удалить многомерный массив?
- Перечислите основные ошибки, связанные с динамической памятью.
- Приведите пример ошибки, связанной с двойным освобождением динамической памяти.
- Приведите пример утечки памяти.
- Как может возникнуть утечка памяти при работе с многомерными массивами?
- Какие способы организации данных можно отнести к фундаментальным?
- Что строят на основе фундаментальных способов организации данных?
- Какие достоинства и недостатки свойственны массивам?
- В чём заключаются проблемы статических и динамических массивов?
- Что такое связанный список? Чем он отличается от массива?
- Какие бывают разновидности связанных списков?
- В чем недостатки списков?
- Как в С и С++ описываются элементы списка?
- Как можно программное реализовать список?
- Какие операции необходимы для работы со списком?
- Что такое дерево?
- Какую роль выполняет корень дерева?
- Какую роль играет понятие поддерева по отношению к дереву?
- Что такое путь на дереве? Глубина дерева?
- Как можно классифицировать деревья?
- Что представляют из себя бинарные деревья?
- Что такое вырожденное дерево?
- Что такое полное дерево?
- Какие операции считаются основными для бинарного дерева?
- Из каких базовых действий строится алгоритм обхода дерева?
- Чем отличаются друг от друга прямой, обратный и симметричный обходы дерева?
- Что такое свойство упорядоченности?
- Как осуществляется программная реализация бинарного дерева?
- Что должен содержать узел бинарного дерева?
- Какие операции над узлами дерева можно отнести к основным?